Complex problems require complex solutions. While this is not always true, it certainly is often enough to inspire the search into automated problem solving. That’s where machine learning comes into play, which, in the best case, allows us to throw a bunch of data at an algorithm and to obtain a solution to our problem in return.
With the advent of deep learning, this trend has been getting a mighty boost, allowing us to (begin to) solve much harder and thereby more interesting problems, like autonomous driving or automated medical diagnosis. In those areas, where human well being is on the line, the algorithms opinions need to be trustworthy and comprehensible. While predictions should be correct, it is even more important to know when they are not, so that one can take appropriate countermeasures, as the real world is messy and often unpredictable, so striving to not make any mistakes ever is probably in vain.
A tragic example of this was the accident of a semi-autonomous vehicle crashing into a white semi truck, mistaking it for a cloud source. Here, an algorithm knowing when it doesn’t know, could have warned the driver to take over. Knowing when you don’t know comes down to placing appropriate confidence in your predictions which is true for humans and algorithms alike. We can also frame this problem from the opposite direction, when talking about the level of confidence as low and high uncertainty.
The mathematical language of uncertainty is probability theory, for which I provided a tiny introduction in my first article of the informal three-part mini-series on probabilistic machine learning of which this article is the third and thereby final part. In the previous article, the second part, I told the story of deep learning and probability theory becoming friends, but we didn’t really get to see how these theoretical insights could be applied in practice, which is the topic of this article.
More precisely, we will be looking at a practical yet powerful way to model a deep neural network probabilistically, thereby transforming it into a Bayesian neural network using a technique called Laplace Approximation. Once we are done with that, we will see how to make use of the newly obtained Bayesian superpowers to solve, or at least mitigate, some problems arising from poor calibration, i.e. being over- or underconfident in ones predictions. I’ll show some results I’ve obtained during the work on my Masters’ thesis through a plethora of interesting figures and visualizations.
Incidentally, the article will also serve as a tutorial to the GitHub repository featuring the code used to obtain all the presented results. If you are uncertain (no pun intended) about your level of background knowledge (of which you certainly need some), head over to the background section of part two to verify or brush up your knowledge, or just press on and see if you get stuck at some point. Also, check out the code that generated all figures in this post if you are interested:
1. Being normal around the extreme
In life as in probabilistic machine learning we are confronted with many open questions, two of which are:
- How to obtain an accurate assessment of my ignorance (estimating the data likelihood and/or parameter posterior in probability theory speak)?
- How to make predictions and take decisions properly grounded in this assessment (integrating out or marginalizing the parameters of our model)?
The answer to the first question is: By modeling it probabilistically. We have already seen this in part one, where we modeled our assumptions and the obtained evidence about the location of a friend on a large ship and I’ve also hinted at it in the second part, where we observed, that the (low dimensional) weight posterior distribution of a neural network has a distinctly Gaussian appearance.
Let’s quickly revisit this second fact here. We already know that the loss function used to train the network has a probabilistic interpretation as the negative logarithm of the likelihood: $E(W)=-\ln p(\mathcal{D}\vert W)$1. When using some form of regularization to prevent overfitting (which we almost always do), it becomes the prior $p(W)$ in the probabilistic framework, and we start working with the posterior instead of the likelihood thanks to Bayes’ Theorem: $p(W\vert\mathcal{D})\propto p(\mathcal{D}\vert W)p(W)$. In other words, the unregularized loss corresponds to the negative log likelihood while a regularized loss corresponds to the negative log posterior. This posterior is what we need to perform Bayesian inference, i.e. to make predictions on new data, like an unseen image of an animal we want to classify. How can we obtain it?
We know that we need to model it probabilistically, i.e. we need to find a probability distribution which captures the important properties of the true, underlying, latent distribution of our model parameters (the weights). Probability distributions come in all kinds of flavors, and we need to strike a balance between expressiveness, which determines how well we can model the true distribution, and practicality, i.e. how mathematically and computationally feasible our choice is.
1.1 Landscapes of loss
To get an intuitive understanding, let’s actually look at a (low dimensional) representation of the likelihood. The likelihood function $L(W)=p(\mathcal{D}\vert W)$ is, as the name suggests, just a function and we can evaluate it at different inputs $W$2. We can, for example, evaluate it at $W^\star$, the weights obtained after training the network. This should yield the highest likelihood and conversely the lowest loss. We can then explore the space around this minimum by taking small steps in one or two (randomly chosen) directions, evaluating $L(W+\alpha W_R)$ or $L(W+\alpha W_{R1}+\beta W_{R2})$ along the way. $W_{R1,2}$ are random vectors of the same size as $W$ and $\alpha$ and $\beta$ are the step sizes. This is what you see below, though we start by visualizing $-\log L(W)$, the loss $E(W)$, first and then move on to the likelihood which is $\exp(-E(W))$.
The so called loss landscape you see above has a few distinctive features3. The most important is, that it is basically a steep valley, at least close to the minimum. This is mostly what allowed our optimizer to find the minimum in the first place, by following the negative gradient in the direction of steepest descent. You can also see that further away from the minimum, small hills begin to appear. The more chaotic the landscape and the further away from the minimum we start our optimization, the harder it will generally be to find the minimum. Now try to think of a probability distribution that could potentially model the shape of this loss landscape. If you can’t quite see it yet, let’s look at the quantity we are actually interested in modeling: the likelihood. All we need to do is to take the exponential of the negative loss, which is what you see on the left below.
And the thing on the right that looks very similar? This is a two-dimensional multivariate normal distribution, aka a Gaussian! Note how the negative exponent has smoothed out those small hills we saw in the previous plot, as large (negative) values get mapped to near zero. In this example, I have estimated the correct parameters for the Gaussian, i.e. the mean and variance, through a least-squares fitting approach. However, so far we have been working with a two-dimensional representation of the loss for visualization purposes while in reality, it has as many dimensions as our network has weights! For the popular ResNet50 architecture for example, that’s more than 25 million! Clearly we need a better approach to estimating the Gaussian parameters, mostly because we can’t gather sufficient loss samples in 25 million dimensional space4.
A bit off topic but still interesting: See the lines below the loss landscape? Those are contour lines, like you would see on a hiking map, and we can use these to compare the loss landscape to the accuracy landscape, which, after all, is the quantity we are actually interested in when confronted with a classification problem. Click on the dropdown menu to select loss and accuracy contour plots and their comparison.
It gets a bit crowded, but what we can make out is, that, at least for low loss/high accuracy regions, the loss contour levels align remarkably well with specific accuracy levels, meaning the loss is a good predictor of classification accuracy. Nice!
1.2 Getting the Gaussian
Back to the topic: How can we estimate the shape of a function in general? Exactly, we can use Taylor expansion. Here is what that looks like:
\[\ln p(W\vert\mathcal{D})\approx\ln p(W^\star\vert\mathcal{D})-\frac{1}{2}(W-W^\star)^TH(W-W^\star)\]Let’s unpack this. On the right we see the posterior we want to estimate. We’ve kept the logarithm when transforming the (negative log) likelihood into the posterior using Bayes theorem but dropped the minus. We expand our Taylor series around the maximum a posteriori estimate $\ln p(W^\star\vert\mathcal{D})$, drop the first order term, because at the extremum, the gradient vanishes, and are left with the second order term. The only unknown quantity here is $H$, the (parameter) Hessian of the (regularized) loss, i.e. of the negative log likelihood or posterior. The Hessian, being the matrix of second order derivatives, describes the curvature of our loss landscape. But wait, didn’t we want to model the loss as a Gaussian? Exactly, but see what happens when we take the exponential:
\[p(W\vert\mathcal{D})\approx\ p(W^\star\vert\mathcal{D})\exp\left(-\frac{1}{2}(W-W^\star)^TH(W-W^\star)\right)\approx\mathcal{N}\left(W^\star,H^{-1}\right)\]Boom, the right hand side becomes the (unnormalized5) probability density function of a multivariate normal distribution!
Okay, so far so good, how to compute the Hessian then? In theory, we could take the gradient of the gradient to obtain it, but in practice this is computationally infeasible for large networks. As it turns out, and this is probably the hardest pill to swallow in this entire article, as I won’t be able to go into any detail why this is so, there is an identical quantity6 which we can compute: The Fisher information matrix F. It is defined as follows:
\[F=\mathbb{E}\left[\nabla_W\ln p(\mathcal{D}\vert W)\nabla_W\ln p(\mathcal{D}\vert W)^T\right]\]In other words, it is the expected value7 of the outer product of the negative gradient of the loss w.r.t. the weights. In one sense, this is easy to compute, because we already have the required gradients from network training, but another problem persists: the size. Just like the Hessian, the Fisher of a deep neural network is of size number of weights x number of weights (which we can also write as $\vert W\vert\times\vert W \vert$) which is prohibitively large to compute, store and invert.
1.3 KFC
There are several ways to shrink the size of our curvature matrix8 of which the simplest is to chop it into layer-sized bits. Instead of one gigantic matrix, we end up with $L$ smaller matrices of size $\vert W_\ell\vert\times\vert W_\ell\vert$ where $L$ is the number of layers in our network and $\ell={1,2,3,…,L}$.
In the figure above you can immediately see the immense reduction in size by comparing the total area of the red squares to that of the initial one. Conceptually, this simplification says, that we assume the layers of the network to be independent from one another. This becomes clearer if you think about the inverse curvature instead, representing the covariance matrix of the multivariate Gaussian we want to estimate, where the off-diagonal terms correspond to the covariances while the diagonal terms are the variances. However, this is still not good if enough.
This brings us to the next simplification, where we also toss out the covariances within each layer, so that we are left with only the diagonal elements of the initial matrix. The first simplification step is referred to as block-wise approximation while the second is called diagonal approximation.
But what if we want to keep some of the covariances? Let’s first think about why this could be helpful. Have a look at the two-dimensional Gaussian below. By changing the diagonal values of the $2\times2$ covariance matrix, we can change the spread, or variance, in $x$ and $y$ direction. But what if the network posterior we are trying to model places probability mass somewhere between those axes? For that, we need to rotate the distribution by changing the covariance, which you can try out by using the third slider.
Now, as I mentioned before, we cannot simply keep the covariances, as the resulting matrices, even using the block-wise approximation, would still be too unwieldy. What we can do though, is an additional decomposition of each curvature block into two smaller matrices called the Kronecker factors using the Kronecker product. The mathematical definition is
\[A\otimes B = \begin{bmatrix}a_{11}B & ... & a_{1n}B\\\vdots & \ddots & \vdots\\a_{m1}B & ... & a_{mn}B\end{bmatrix}\]but it’s easier to think about it visually. For example, if $A$ is a $2\times2$ matrix, we can color $a_{11}$ to $a_{22}$ with a different color and then, each of the colored squares is multiplied with every of the four gray squares representing $B$ and placed in the corresponding corner of the resulting matrix.
Even for this toy example you can see that we have reduced the $4\times4$ matrix with $16$ elements to two $2\times2$ matrices with $4+4=8$ elements. Once we use the curvature matrices as covariance matrices, we will have to invert them though, but very conveniently, the inverse of the Kronecker product is the same as the Kronecker product of the inverse factors: $(A\otimes B)^{-1}=A^{-1}\otimes B^{-1}$!9
This final approximation is called Kronecker factored curvature, KFC, and yields a substantially better approximation to the entire curvature matrix compared to a simple diagonal approximation at only a moderate increase in memory requirements.
1.4 Appearing more confident than you are
There is one last obstacle we need to clear before we can use our newly obtained curvature approximation. While in theory a matrix computed by an outer product like the Fisher should always be invertible, in reality this might not necessarily be the case for numerical reasons. But there are two more reasons why we might want to alter those matrices:
- Our approximations, while necessary to render the problem tractable, could have introduced an unwarranted amount of uncertainty in some directions.
- The idea to approximate the weight posterior of our network by a multivariate Gaussian distribution could be flawed, which could happen if the true posterior is not bell shaped or only so in certain directions but not in others. If you have another look at the comparison of the exponential negative loss and the Gaussian above, you can already see that they are only similar, but not identical.
To combat these problems, we can use regularization. In deep learning, the most well known form of regularization is weight decay aka $L_2$-regularization. In the previous article, we have already seen that it has a probabilistic interpretation as a Gaussian prior. This can be easily extended to our case, by adding a multiple of the identity matrix to the curvature matrix. Here is why: Through the introduction of a prior, we are now dealing with the posterior instead of the likelihood. So far, we have been computing the Fisher of the log likelihood, i.e. $F[\ln p(\mathcal{D}\vert W)]$, as explained before.
If we now want to compute the Fisher of the log posterior, $F[\ln p(W\vert\mathcal{D})]$, we can make use of Bayes’ theorem and write
\[F[\ln p(W\vert \mathcal{D})]\propto F[\ln p(\mathcal{D}\vert W)+\ln p(W)]=F[\ln p(\mathcal{D}\vert W)]+F[\ln p(W)]\]Due to the logarithm, the prior is added instead of multiplied and we end up with a sum of the known curvature of the log likelihood (the first term) and the curvature of the log prior (the second term), which we will replace by an isotropic Gaussian, i.e. a Gaussian with identical variance in all dimensions and zero covariance. To get rid of the proportionality sign, we can simply add a multiplicative constant an arrive at
\[\hat{F}=NF+\tau I\]where $\hat{F}$ is the Fisher of the log posterior, i.e. our new, regularized, Fisher (playing the part of the curvature). Now we need to choose reasonable values for our two new parameters $N$ and $\tau$. Staying in the theoretical probabilistic framework, reasonable choices would be the amount of weight decay used during training for $\tau$ and the size of the dataset for $N$.
However, the former will neglect the influence of any other form of regularization like dropout or data augmentation while the latter is only a crude approximation of the evidence $p(\mathcal{D})$. In practice, we will treat $N$ and $\tau$ as hyperparameters and optimize for good accuracy and calibration on a validation set.
Again, an intuitive understanding of the influence of those parameters on the shape of the posterior can be gained through an interactive visualization:
At fist glance, both parameters seem to do a very similar thing. But while both do indeed decrease the variance, $N$ additionally decreases the covariance by the same amount, so the shape of the Gaussian gets preserved. On the other hand, increasing $\tau$ reduces the influence of the covariance, so the Gaussian becomes more circular and less elliptic.
This is an important observation, as we can loose all of the potential benefit of modeling the covariances using, for example, the Kronecker factorization, by then adding a large multiple of the identity matrix to it. In the limit, i.e. when setting the hyperparameters to very large values, we recover the deterministic network, as we have effectively reduced the Gaussian to its mean, which we set to $W^\star$ from the beginning.
1.5 Integration with Monte Carlo
Now that we finally have the posterior $p(W\vert\mathcal{D})=\mathcal{N}(W^\star,\hat{F}^{-1})$ we can perform inference on new unseen data $\boldsymbol{x}^\star$. In the probabilistic context, this is done through marginalization:
\[p(\boldsymbol{y}^\star\vert\boldsymbol{x}^\star)=\int p(\boldsymbol{y}^\star\vert\boldsymbol{x}^\star,W)p(W\vert\mathcal{D})\mathrm{d}W\]Here, we run into another problem: This integral is intractable. While we are fortunate to have chosen a Gaussian as posterior, which we could integrate if needed, the neural network $p(\boldsymbol{y}^\star\vert\boldsymbol{x}^\star, W)$ doesn’t provide this courtesy. Was all our hard work in vain then? By no means! Thanks to Monte Carlo, we can perform approximate Bayesian inference through sampling.
\[\int p(\boldsymbol{y}^\star\vert\boldsymbol{x}^\star,W)p(W\vert\mathcal{D})\mathrm{d}W\approx\frac{1}{T}\sum_{t=1}^Tp(\boldsymbol{y}^\star\vert\boldsymbol{x}^\star,W_t)\]The weight samples $W_t$ can be drawn efficiently from our posterior s.t. $W_t\sim\mathcal{N}(W^\star,\hat{F}^{-1})$. We then load them into our network, perform a standard forward pass on the new input to obtain the output and repeat this a couple of times. By averaging the output over all evaluations, we obtain the final result. In the limit, approaching an infinite number of weight samples, we reclaim the solution of the integral, but in practice, around $30$ such samples already lead to significantly improved results as we will see in the next section.
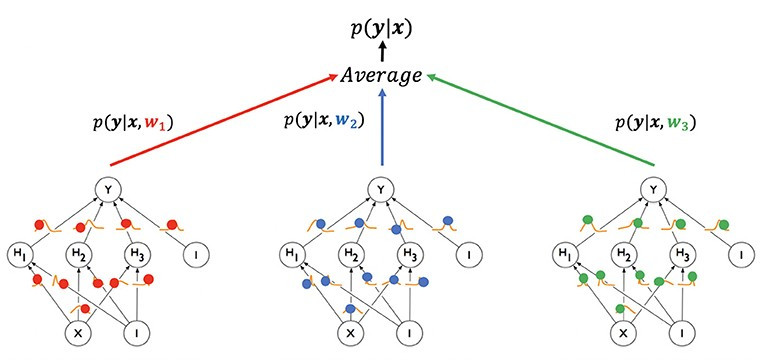
2. Into the wild
It’s time to put this Gaussian to work now. As mentioned in the beginning, there are many possible applications, so we will limit ourself to three:
- Calibration: Using Bayesian inference, can we reduce the severe and potentially dangerous overconfidence of modern deep neural networks?
- Out-of-distribution detection: By looking at the (calibrated) uncertainty of our networks predictions, can we separate known from unknown data? In other words, can the network detect deviations from the data it was trained on?
- Adversarial attacks: Given an adversary, trying to fool our network into predicting rubbish, can we make the network more resilient to such an attack?
2.1 Wait, is that really a Ferrari?
To become better calibrated, we first need to know where we stand. In the previous article, we defined good calibration as the notion, that the networks confidence and accuracy should match, meaning that high and low confidence should go along with high and low accuracy respectively.
If you think back at the first article, good calibration is actually the magic wand that can appease the two opposing factions in probability land—the Bayesians and the Frequentists—because it only occurs if the empirical frequency of being correct (accuracy) matches the belief about it (confidence).
2.1.1 Reliability diagram
Let’s see how we can put this more quantitatively. With the (average) accuracy defined as the fraction of correctly classified examples and the confidence simply being the probability our network assigned to the predicted class, the average calibration error is the difference between accuracy and confidence averaged over all examples, usually the validation or test images from our dataset.
If it is greater than zero, the network is overconfident while a value smaller than zero indicates underconfidence. This metric can be misleading though, because a classifier which is overconfident on one half of the inputs and underconfident on the other could appear to be perfectly calibrated.
Instead, we can partition the predictions into bins, as is done in histograms, based on their assigned confidence. Then, we compute an average calibration error for each bin and weigh it by the number of examples in it. Averaging these weighted (absolute) errors results in the so called expected calibration error all of which you see visualized below.
On the horizontal axis, you see the confidence, partitioned into 10 equally spaced bins. The blue bars represent the average accuracy in each bin while the average calibration error is shown on top as red bars, signifying the calibration gap to perfect calibration. If you hover over each bin, you see the average accuracy and average calibration error. You can also disable parts of the plots by clicking on the legend items. For example, if you disable the accuracy bars, the average calibration error becomes more visible, with values below zero showing underconfidence and those above zero denoting overconfidence as explained above. A perfectly calibrated network would follow the black dashed line.10
2.1.2 Calibration curve
This type of visualization is useful to study a single network in detail, but comparing multiple networks or calibration techniques is difficult. To do so, we can replace the accuracy on the vertical axis by the average calibration error and plot it for each confidence interval. The networks calibration can then easily be identified as underconfident for values below the horizontal line at zero and overconfident for those above.
Here, we are comparing some networks from the DenseNet family with increasing depth11. The horizontal axis is shown in logit scale which provides more space for the critical high-confidence regime. You can enable the error range to see the minimum and maximum calibration error to expect from the shown networks.
Now let’s see what happens if we use the same networks but employ our Bayesian approach from the previous section.
This looks a lot better! Especially the overconfident behavior could be reduced significantly from a worst case average calibration error of more than $11\%$ to around $3.5\%$, which you can also see in the much narrower error range. This could be used to give a confidence interval of, say, $\pm4\%$ when making predictions and taken into account when deciding whether human intervention is necessary. Overconfidence is especially critical to fix, as it can result in dangerous behavior when exhibited by autonomous systems like robots and cars. The underconfident behavior could also be slightly reduced, though.
The final comparison we can make is between the different curvature estimators. Remember that we introduced the simple diagonal estimator (DIAG) that ignored all covariances and a second one that used Kronecker factored approximate curvature (KFAC) where covariances within each layer were retained. SGD, referring to stochastic gradient descent, is the standard neural network.
In this example we can see, that KFAC slightly outperforms DIAG, though this is not always the case and the reason for this is still an open research question. Intuitively one would expect, that a better posterior approximation should also always yield more accurate Bayesian inference which in turn should result in increased performance across different tasks. Here are some more uncalibrated network architectures compared, just for fun.
2.2 Knowing when you don’t know
Well calibrated uncertainty estimates are useful in and of itself but can also be seen as a stepping stone to more elaborate applications like anomaly detection. An anomaly can be anything out of the ordinary, where ordinary is defined by the data used for training the network. In a medical setting, this could be a change in the measured body functions which an algorithm trained to recognize diseases didn’t encounter before or an animal crossing the road observed by the object recognition subsystem of an autonomous vehicle which doesn’t fit in the known categories like car, road and pedestrian.
What we want in these settings is an algorithm that provides correct predictions with high confidence on familiar inputs and low confidence predictions on unfamiliar ones it cannot classify correctly.


To test this, we can for example train a neural network on photographs of objects and then serve it some photographs of new objects. Or, we can replace the photographs by paintings or artistic impressions of objects, which is the approach I’ve chosen in my work. Such unknown data comes from a so called out-of-domain distribution which is not part of the domain the network was trained on, in this case photographs vs paintings.
2.2.1 Entropy histogram
An intuitive way to visualize the networks behavior is to produce a histogram of the networks predictive uncertainty, one for the known and one for the unknown data, and overlay them. We’ve talked about predictive uncertainty in the previous article, but you can simply think about it as the opposite of confidence, but on a solid information theoretic footing, as it is measured as the entropy of the networks output distribution.
The entropy of a probability distribution (and keep in mind that a neural network provides a (uncalibrated) categorical probability distribution over the object classes as its output) can be interpreted as the average amount of information it provides, which can be understood as the level to which the outcome of an experiment would surprise the observer.
When flipping a fair coin, the expectation to see heads is identical to that of tails, which is why a fair coin gets assigned maximum entropy. But if the coin is biased, having e.g. a much higher probability to show heads than tails, a knowing observer would be surprised to see it land tails when flipping it. Consequently, the entropy of a biased coin is lower than that of a fair one.
As can be seen, a standard network is not able to separate the known and unknown data. While the average and maximum entropy for the unknown data is higher, there is a large overlapping area where separation is impossible. Again, let’s see how our Bayesian neural network performs.
And again, the Bayesian approach saves the day, achieving almost perfect separation of known and unknown examples. What that means is, that we could now use a threshold slightly above $4$ to raise the alarm for any prediction producing a higher value.
2.2.2 The empirical cumulative distribution function
As was the case for the calibration experiments, this is a great approach to scrutinize a single network, but unsuited for comparing several architectures or curvature estimators. To do so, we need a employ a slightly more complex procedure. We keep the predictive entropy on the vertical but use the inverse empirical cumulative distribution function (ECDF) on the horizontal.
This sounds scary, but let’s break it down. First, we need to understand the cumulative distribution function. The CDF of a random variable expresses the probability (on the vertical axis) that this random variable will take on a value less than or equal to any value on the horizontal axis. For example, imagine we are modeling the temperature of tomorrow. Having gathered the data of last week and modeled it by a probability distribution, using its CDF we can answer the question “What’s the probability that it won’t get warmer than 30 degrees Celsius?” by looking for the function value at 30. We could also have sticked to the probability mass function of our probability distribution and integrated between absolute zero and 30 degrees.
The empirical version of the CDF simply provides the empirical frequency instead of the probability of an event happening. Finally, the inverse allows us to ask the for the probability (or frequency) that our probability distribution takes on a value greater instead of less or equal the value on the horizontal axis. Let’s have a look at it now.
What you see is the same data as in the histogram shown before. Focusing on the solid lines, we see that the Bayesian approach (DIAG) exhibits high uncertainty for all of the unknown examples (i.e. an inverse ECDF value of $1$ for entropy values of at least around $4.7$) while the standard network (SGD) only classifies around $6\%$ of the unknown data with such a high uncertainty.
This new visualization allows us additionally to look at the uncertainty on the known data (the dashed lines), which should correspond to the networks accuracy (so no under- or overconfidence). We see that it is a lot lower compared to the unknown data for both the standard and Bayesian network. This is important, as we don’t want to achieve high uncertainty on the unknown data simply by raising the bar everywhere s.t. our network predicts all kind of data with high uncertainty. Finally, we can also see that the KFAC estimator again slightly outperforms the DIAG estimator.
Similar to the calibration experiments, we can also directly compare different networks. Let’s first have a look at the non-Bayesian variants.
Interestingly, deeper networks seem to exhibit greater overconfidence in the ResNet family, hindering them to properly separate the known from the unknown data, a trend we see continued after having applied our Bayesian transformation. However, regardless of depth, all networks substantially benefit from the Bayesian treatment.
Under attack
The final application I’d like to showcase is the increased resilience of Bayesian neural networks to adversarial attacks.
An adversarial attack tries to alter the algorithms output either arbitrarily away from the intended one or even steered into the direction of a desired output. Those attacks are usually divided into white and black box attacks, depending on the access the attacker has to the internal workings of the algorithm.
For neural networks, a simple attack mechanism is the Fast Gradient Sign Method. While we follow the negative gradient of the loss w.r.t. the weights of the network during training in order to minimize it, the FGSM computes the gradient of the loss w.r.t. the pixels of the input image to find which pixels altered by what amount would result in the greatest increase of the loss.
For each color channel of each pixel we thus obtain a value which, multiplied by a step size can be added to the image in order to mislead the network. Often, very small changes, imperceptible to the human eye, are sufficient to reduce a networks predictions to random noise.
In essence, we create a form of out-of-domain data, as in the previous section, but we can control its “differentness” by adjusting the step size. The question is then, how quickly we can detect such an attack, by looking at the increase of network uncertainty.
While both the standard network as well as the Bayesian variants show an increased uncertainty with increasing change, the Bayesian networks rise faster and to a higher level, resulting in higher sensitivity to malicious tempering of the inputs. This could be exploited by comparing the predictive entropy of a new input to the average uncertainty of the network on previous inputs to determine the likelihood of an attack.
Wrapping up
You have made it till here and I would like to congratulate you for this feat! There has been a lot of highly condensed information in this article in an attempt to summarize most of the important insights I gained while working on the topic. I hope it wasn’t too hard to follow and you were able to take something away for your on projects. If you are eager to get your fingers dirty after all this theory definitely check out the GitHub repository. Have a pleasant day feel free to drop me a comment if anything was left unclear or you spot a mistake. Cheers!
-
Please refer to part two for an introduction of the notation. ↩
-
Make no mistake, even though the likelihood is the probability distribution over the data (given the weights), we are still trying to find the weights that best explain the data and not the other way round. ↩
-
Here are some more examples, if you are interested as well as the paper describing the approach. ↩
-
Have a look at the curse of dimensionality. ↩
-
In practice, we don’t care much about the normalization factor, because under most conditions, the posterior distribution is asymptotically normally distributed as the number of data points goes to infinity. ↩
-
This is only the case for networks that use piece-wise linear activation functions (like ReLU) and exponential family loss functions (like least-squares or cross-entropy). ↩
-
The expectation is taken w.r.t. the output distribution of the network. If the data distribution is used instead, one obtains the empirical Fisher which doesn’t come with the same equality properties to the Hessian compared to the “true” Fisher. ↩
-
I’ll be using this term instead of Hessian or Fisher (or Generalized Gauss-Newton for that matter), because for our purposes they are equivalent and can all be interpreted as the curvature of the function they represent. ↩
-
Unfortunately, this equality can not generally be maintained in expectation s.t. $\mathbb{E}[A\otimes B]\neq\mathbb{E}[A]\otimes\mathbb{E}[B]$. ↩
-
To get meaningful results, all evaluations where made on a held-out test set that was neither used for training nor hyperparameter optimization, in other words, the network hasn’t seen the images before. ↩
-
Double click on an item in the legend to disable all others. Double click on the plot afterwards to adjust the axes ranges to the data currently shown. ↩